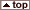
by
Hope Poteat Mizzell
Bachelor of Science
University of South Carolina, 1993
Submitted in Partial Fulfillment of the
Requirements for the Degree of Master of Science
in the Department of Geography
University of South Carolina
1999
_______________________ ________________________
Department of Geography Department of Geography
Director of Thesis 2nd Reader
_______________________ ________________________
Department of Geography Dean of the Graduate School
TABLE OF CONTENTS
ACKNOWLEDGEMENTS .....................................................................
ii
ABSTRACT ..............................................................................................iii
LIST OF TABLES ....................................................................................vii
LIST OF FIGURES ..................................................................................viii
LIST OF APPENDICES ...........................................................................x
INTRODUCTION
1.1. Scope ..............................................................................................1
1.2. Significance ......................................................................................3
1.3 Literature Review
.............................................................................5
1.3.1 Past Research
.........................................................................5
1.3.2 Radar
Limitations ....................................................................6
1.3.3 Rain Gauge
Measurement ........................................................8
1.3.5 Interpolation
Techniques ..........................................................9
1.4 Methods
and Organization ...............................................................11
METHODOLOGY
2.1 Spatial
and Temporal Characteristics of the Research .....................12
2.2 Data ..............................................................................................12
2.2.1
Precipitation Events ..............................................................12
2.2.2
WSR-88D Estimated Precipitation Data ...............................13
2.2.3
Manual and Automated Gauges ...........................................15
2.2.4
Inverse Distance Weighting and Kriging .............................. 16
2.3 Radar and Gauge
Comparison ......................................................17
2.3.1 Geographic Information System .........................................17
2.3.2 Loose Coupled Statistical Model .......................................19
2.3.3 Radar and Tipping Gauge Analysis ...........................
.........20
2.3.4 Synoptic Classification and Influence ..................................20
RESULTS
3.1 Interpolation
Validation and Estimation .........................................22
3.2 Radar Gauge Comparison
............................................................22
3.2.1
Stratiform Events .................................................................23
3.2.2
Convective Storms .............................................................26
3.2.3
Tropical System Event ........................................................29
3.3 Relationship Between Radar-Gauge
Differences for seven events.........31
DISCUSSION
4.1 Utility of the Loosed Coupled GIS ................................................33
4.1.1 Reliability
of the ANOVA and Regression models ...............33
4.2 Radar Rainfall Error Sources
........................................................34
4.2.1 Reflectivity
Estimate ............................................................34
4.2.2 Z-R Relationship
.................................................................36
4.2.3 Distance
from Radar ............................................................36
4.2.4 WSR-88D
Calibration ........................................................37
4.3 Event Consistency ........................................................................38
CONCLUSION
5.1 Radar's Performance .................................................................39
5.2 Physical Factors .........................................................................40
5.3 Gauge and Interpolated
Techniques ............................................40
5.4 Expectations of Decision-Makers
and Research Community ...............40
5.5 Real-Time Calibration With
Automated Gauges ..........................41
5.6 Future Research .........................................................................41
REFERENCES ....................................................................................43
TABLES ..............................................................................................47
FIGURES ............................................................................................55
APPENDICES ....................................................................................95
I came to realize throughout the project how fortunate I was to be surrounded by support from family, co-workers, and my graduate school department. A sincere thanks is conveyed to family, friends, and colleagues that made my thesis possible.
First and foremost, I would like to express my gratitude to Dr. Greg Carbone. He has been there for me since the first day I walked into his office ten years ago as an undergraduate. I will always be grateful for his teaching, guidance, and friendship. In addition, I would like to thank Dr. Robert Lloyd and Dr. Michael Hodgson for their participation and assistance.
I appreciate the participation of Lexington County Department of Planning and Development. The project would have not been possible without the volunteer weather observers. Thanks to each of you that diligently recorded daily rainfall for over two years.
I thank my friends at the South Carolina Department of Natural Resources, Southeast Regional Climate Center and National Climatic Data Center for funding the project and for their encouragement. I especially recognize Dr. Michael Helfert for his confidence and persistence in making sure I completed this degree. I deeply thank him for his daily support and interest in my quest for knowledge.
I also want to thank my parents for their unconditional love and support. Thank you for giving me a solid foundation filled with so many opportunities. Even though my mom has passed away her encouragement and strength were with me every step of the way. For my dad, thank you for always being there for me and for giving me the opportunity to succeed.
Thanks also to my immediate family especially my parents-in-law. I am blessed to have such a close and loving family.
Most importantly, I want to express my thanks and love to my husband, Tony. Your dedication to me has helped me overcome the rough times and shine through the good ones. Thank you for your patience, love, devotion, and for helping make all my dreams come true.
ABSTRACT
The deployment of the National Weather Service Weather Surveillance Radar-1988 Doppler (WSR-88D) has provided an improved tool for monitoring precipitation distribution. Because the WSR-88D can estimate rainfall at high spatial and temporal resolution, it has great potential for meteorological and hydrological modeling. Unfortunately, a number of factors introduce discrepancies between radar rainfall estimates and actual rainfall at the Earth's surface. In this paper, I compare rainfall estimates from the Columbia Airport National Weather Service WSR-88D with precipitation recorded by 62 standard rain gauges and 10 tipping gauges in Lexington County, South Carolina. The study included 7 precipitation episodes that covered a variety of synoptic types such as convective storms, tropical systems, and stratiform events. Discrepancies between the gauge and radar were analyzed by storm event to determine what potential synoptic or inherent factors caused the differences. The analysis used a Geographic Information System and SAS regression and ANOVA models.
Results show that the radar consistently underestimates precipitation, independent of the storm type. When all the storms were combined, agreement between precipitation estimates from gauges and radar was weak, with the total for the gauges being 20.9 inches on average and that for the radar 8.1 inches on average, a difference of 61%. However, when the storms were considered individually, two storms had a radar-gauge difference of less than 5%. The degree of underestimation varied with storm intensity, duration and type. The radar's performance was the weakest during the three stratiform storms. The underestimation of 75% of the gauge data was probably attributed to the light, widespread rain and small dropsize. Overall, the convective events had the highest average percent accuracy with the radar estimating 96% of the gauge data. However, the radar estimation accuracy was not consistent. The factors during these convective systems which probably had the greatest effect on radar measurements were enhancement of reflectivity by hail and larger than average raindrops and diminution of estimation by small drops and downdrafts. The radars estimated precipitation during the passage of Tropical System Earl, September 3-4, 1998, ranged from 20% to 86% as compared to the gauges. The abundance of moisture associated with tropical maritime air makes it difficult for the radar to determine a representative reflectivity.
The results from this study indicate that the radar can't yet provide the spatial distribution of surface rainfall that is needed for many operational and research applications. Because of the great variability in the intensity and distribution of precipitation, more radar-gauge comparisons should be conducted covering a larger number of storms. Future research has been stimulated by these results which include analysis of the radar level II base reflectivity data to determine whether the error sources were caused by inaccurate reflectivity values, an incorrect Z-R conversion, or a combination of the two. Results from both studies will ultimately be coupled with efforts to eliminate the systematic biases of the radar and improve quantitative precipitation forecasts.
Chapter 3
3.1 Interpolation Error Results from IDW and Kriging for Each
Event
3.2 Rainfall Summary for Each Event
3.3 Root Mean Square Error For Each Event
3.4 Regression Model Output: R2 and F Statistic
3.5 RMSE and Regression Output for Twelve Mile Creek and
Fourteen Mile Creek Basin
Chapter 1
1.1 Radar Scan Angles and Volume Scanning Technique
1.2 Example of Radar Bin and Reflectivity Correction Techniques
1.3 Study Area: Gauge Locations in Lexington County, South
Carolina
Chapter 2
2.1 Description of Tipping Gauge Calibration and Recording
Techniques
2.2 Conceptual Model for Analysis
2.3 Example of Daily Weather Charts and NWS State Weather Summary
Chapter 3
3.1 Zones Used For Analysis
3.2 September 24-29, 1997 Gauge Precipitation and Radar Precipitation
3.3 September 24-29, 1997 Difference Between Radar Precipitation
and Gauge Precipitation (Radar - Gauge)
3.4 September 24-29, 1997 Tipping Gauge Precipitation and Radar
Precipitation
3.5 September 24-29, 1997 Difference Between Radar Precipitation
and Tipping Gauge Precipitation (Radar - Tipping
Gauge)
3.6 January 22-23, 1998 Gauge Precipitation and Radar Precipitation
3.7 January 22-23, 1998 Difference Between Radar Precipitation
and Gauge Precipitation (Radar - Gauge)
3.8 January 22-23, 1998 Tipping Gauge Precipitation and Radar
Precipitation
3.9 January 22-23, 1998 Difference Between Radar Precipitation
and Tipping Gauge Precipitation (Radar - Tipping Gauge)
3.10 February 3-5, 1998 Gauge Precipitation and Radar Precipitation
3.11 February 3-5, 1998 Difference Between Radar Precipitation
and Gauge Precipitation (Radar - Gauge)
3.12 February 3-5, 1998 Tipping Gauge Precipitation and Radar
Precipitation
3.13 February 3-5, 1998 Difference Between Radar Precipitation
and Tipping Gauge Precipitation (Radar - Tipping Gauge)
3.14 October 22-26, 1997 Gauge Precipitation and Radar Precipitation
3.15 October 22-26, 1997 Difference Between Radar Precipitation
and Gauge Precipitation (Radar - Gauge)
3.16 October 22-26, 1997 Tipping Gauge Precipitation and Radar
Precipitation
3.17 October 22-26, 1997 Difference Between Radar Precipitation
and Tipping Gauge Precipitation (Radar - Tipping Gauge)
3.18 April 8-9, 1998 Gauge Precipitation and Radar Precipitation
3.19 April 8-9, 1998 Difference Between Radar Precipitation and
Gauge Precipitation (Radar - Gauge)
3.20 April 8-9, 1998 Tipping Gauge Precipitation and Radar Precipitation
3.21 April 8-9, 1998 Difference Between Radar Precipitation and
Tipping Gauge Precipitation (Radar - Tipping Gauge)
3.22 August 9, 1998 Gauge Precipitation and Radar Precipitation
3.23 August 9, 1998 Difference Between Radar Precipitation and
Gauge Precipitation (Radar - Gauge)
3.24 August 9, 1998 Tipping Gauge Precipitation and Radar Precipitation
3.25 August 9, 1998 Difference Between Radar Precipitation and
Tipping Gauge Precipitation (Radar - Tipping Gauge)
3.26 Extreme Overestimated WSR-88D Grids During April and August
Storms
3.27 September 3-4, 1998 Gauge Precipitation and Radar Precipitation
3.28 September 3-4, 1998 Difference Between Radar Precipitation
and Gauge Precipitation (Radar - Gauge)
3.29 September 3-4, 1998 Tipping Gauge Precipitation and Radar
Precipitation
3.30 September 3-4, 1998 Difference Between Radar Precipitation
and Tipping Gauge Precipitation (Radar - Tipping Gauge)
3.31 ANOVA Results - Relationship Between Seven Events
Chapter 2
2.1 C program to decode binary WSR-88D data
2.2 Avenue Script for Universal Kriging Interpolation Technique
2.3 SAS ANOVA for Testing Significance of Interpolation Technique
Errors
2.4 Avenue Script for Computing Root Mean Square Error
2.5 Avenue Script for Summarizing by Zone
2.6 SAS Regression Model
2.7 SAS ANOVA for Testing Significance of Radar-Gauge Differences for
All Events
Decision-makers and researchers require accurate
spatial and temporal precipitation estimates. High resolution flood
and drought monitoring, management of agricultural crops, forecasting hydroelectric
power, assessments of extreme precipitation events, and other water resources
management applications all require reliable precipitation inputs (Real-Time
Calibration of Radar Precipitation Estimates, 1998). For a
century, the rain gauge has been the standard for measuring surface rainfall
and is often assumed to be "ground truth" because of its long service and
widespread use (Hunter, 1996). However, gauges produce point measurements
that are assumed to represent a larger area.
The United States meteorological network consists
of about 8,000 daily rainfall recording stations (Groisman and Legates,
1994). Distances between stations often exceed 60 miles (Real-Time
Calibration of Radar Precipitation Estimates, 1998) providing inadequate
spatial sampling. Gauge measurement errors produced by wind/turbulent
losses (Yang et al. 1998; Groisman and Legates, 1994), gauge wetting, splash
into and out of the gauge (Brandes and Wilson, 1998), and evaporation (Austin,
1987) compound the estimation problem.
The recently installed network of WSR-88D
Next Generation Weather Radars (NEXRAD) attempts to solve these problems
by providing a temporally continuous spatial estimate of rainfall.
The WSR-88D precipitation processing system brings a dramatic advancement
to operational radar estimated precipitation in the United States.
The weather radar is capable of providing high resolution rainfall estimates
up to 124 nautical miles from the radar site (Cammarata, 1998). Unfortunately,
this land-mark development suffers from limitations inherent to the use
of radar to estimate precipitation, limitations that have persisted despite
50 years of field research (Hunter, 1996).
Radars do not directly measure rainfall amounts,
but estimate rainfall rate, R (mmh-1), via an empirical relationship with
the radar reflectivity factor, Z (mm6m-3) (Cammarata, 1998). The
relationship is complex, nonlinear, and inexact. Rainfall rates are
proportional to the volume of the raindrops, but reflectivity is proportional
to raindrop surface area (Burgess and Ray, 1992). Therefore, a raindrop
size distribution must be assumed to convert from reflectivity to rainfall
rate. Reflectivity is converted into a rainfall rate by the
Z-R relationship using the formula:
Z= aRb
where a and b are coefficients. A significant problem is that
the Z-R relationship values vary as a function of storm types because of
the differences in raindrop size distributions (Joss and Lee, 1995).
Additional factors complicating the Z-R relationship include: beam attenuation
(Austin, 1987; Hunter, 1996), range effects (Hunter, 1996), temperature
and vapor gradients (Joss and Lee, 1995; Hunter, 1996), hail and vertical
air motions (Austin, 1987), accretion and evaporation (Wilson, 1979).
Although radar has been used experimentally
for nearly 30 years to measure rainfall, operational implementation has
been slow even with the advent of the WSR-88D (Wilson et al. 1979).
Consequently, assessment of radar accuracy has also lagged. Successful
assessment requires comparison of radar estimates with rain gauge measurements
(Wilson et al. 1979).
How accurate are WSR-88D radar rainfall estimates compared to
precipitation measured in a dense rain gauge network? This study
addressed that question through detailed and quantitative comparisons of
rain gauge and radar records in Lexington County, South Carolina.
The project used a loose coupled Geographic Information Systems (GIS) approach
to model the relationship between the gauge and radar data. The study
included 7 precipitation events that covered a variety of synoptic types
such as convective cells, tropical systems, and stratiform events.
Discrepancies between the gauge and radar were analyzed by storm event
to determine what the potential synoptic or inherent factors were causing
the differences.
Although the network of WSR-88D radars
provides detailed rainfall information that is readily available to the
user, these data are not being used to the fullest extent.
Confusion and misunderstanding about the ability of the radar to measure
rainfall and about the factors that contribute to errors lead to this underutilization
of the data. There is an increasing amount of research relating to
the topic of radar-rain gauge comparison. However, as Austin (1987)
emphasized, due to the great variability in the intensity and structure
of rain events, more radar-gauge comparisons should be made in order to
cover a larger number of storms for different geographical locations.
It is important to have an understanding of the physical factors impacting
the radar's accuracy to make the best possible estimate of surface rainfall
from the radar and gauge data available for the particular event.
The study was also triggered by a previous analysis
conducted by the National Climatic Data Center (NCDC). NCDC compared
NEXRAD estimated storm total precipitation with rain gauge measured total
precipitation for 5 events. The Columbia Metropolitan Airport WSR-88D
radar was analyzed during Tropical Storm Jerry, August 1995. The
results indicated that out of 6 radars (Columbia, Houston, Kansas City,
Melbourne, Mobile, and Slidell) the Columbia radar was second worst in
estimating rainfall. Since this study did not have a dense network
of rain gauges for comparison a new study was needed to analyze the Columbia
radar over an extended time period.
1.3.1 Past Research
Several investigators have analyzed the relationship
between radar and rain gauge precipitation totals (Woodley and Herndon,
1970; Wilson and Brandes, 1979; Austin, 1987; Brandes and Wilson, 1988;
Wilson et al., 1997). Most studies used National Weather Service
(NWS) rain gauges with densities exceeding 40 miles. Wilson, French,
Bhaskar, and Anderson (1997) conducted a study using a network of 30 high
resolution rain gauges in Jefferson County, Kentucky for 1 precipitation
event. While other studies were not limited to 1 event most did not
cover a variety of synoptic conditions. Austin (1987) conducted a
radar-gauge comparison using 33 NWS gauges for 9 convective storms and
6 stratiform storms in New Hampshire. Wilson and Brandes (1979) provide
a thorough review of various studies including extensive bibliographies.
Radar-gauge comparison studies have yielded varying
results ranging from a 10% to 60% overall precipitation difference.
As emphasized by Austin (1987), the extent to which results from 1 study
can be applied to other geographical locations is questionable. Minimal
analysis has been conducted in the Southeast. Lott and Sittel (1996)
compared radar estimated precipitation with rain gauge measured precipitation
for 5 events, 4 of which were in the Southeast. There are questions
about the reliability and usefulness of analysis on 1 or 2 event episodes.
This project proposed a unique analysis by performing a radar gauge
comparison using a dense network of gauges over a variety of synoptic events
in the Southeast United States.
1.3.2 Radar Limitations
The WSR-88D radar brings a definite advancement to
rainfall estimates across a continuous surface when compared to earlier
radars and the sparsely represented rain gauge network. However,
the WSR-88D radar experiences significant limitations inherent to the use
of a radar to estimate precipitation. A significant problem is attributed
to the non-linear relationship between radar reflectivity and rainfall
rate at the surface (Hunter, 1996). The radar processes a returned
reflectivity from the precipitation droplets in the volume of the radar
beam. Rainfall rates are proportional to the volume of the raindrops,
while the reflectivity is proportional to the raindrops' surface area.
Therefore, a raindrop size distribution must be assumed to convert from
reflectivity to rainfall rate. If the raindrop size distribution
were exponential and known, there would be no error in the radar rainfall
estimates (Wilson, 1979). However, the raindrop size distribution
is rarely known because it varies widely as a function of storm types.
Wilson and Brandes (1979) suggest that even for similar type storms in
the same geographical area variations in the Z-R relationship may exist.
Thus, an average empirical Z-R relationship must be used. Conversion
from reflectivity to rainfall rate are accomplished using a Z=300R1.4
(Burgess and Ray, 1992) although an alternative equation Z=250R1.2 (Cammarata,
1998) may be used during tropical events with special permission of the
WSR-88D Operational Support Facility (OSF) in Norman, Oklahoma (Burgess
and Ray, 1992). Another potential relationship that can be used for
intense convective cells is Z=400R1.3 (Austin, 1987), however, not all
forecast offices implement this formula. A single Z-R relationship
is inadequate to provide the appropriate conversion for all precipitation
events. Error can occur in the conversion even using the relationships
by storm type. Woodley and Herndon (1970) indicate that convective
rainfall estimates in the southern United States using the standard Z=300R1.4
were extremely underestimated.
Another factor on the radar estimate of precipitation
is the effects of precipitation with height. The curvature of the
earth impacts the radar observation height. If either the nature
or intensity of the precipitation varies with height then the radar estimates
may not represent surface rainfall (Joss and Lee, 1995; Austin, 1987).
Significant growth of raindrops by accretion within 1.2 miles of the surface
can cause the radar to underestimate the rainfall (Austin, 1987).
Evaporation at lower levels can cause the radar to overestimate surface
rainfall (Austin, 1987).
Several factors during convective storms can distort
the radar signal. This could be a major factor for this study because
convective storms are the primary source of rainfall during the summer
months. The presence of hailstones in convective storms causes a
sharp increase in reflectivity as compared to the water equivalents (Austin,
1987). Strong vertical air motions associated with convective storms
alter the fallspeed of the raindrops (Austin, 1987). Updrafts decrease
the signal returned to the radar and downdrafts increase the signal (Battan,
1976).
Anomalous propagation is a limiting factor which
occurs when large vertical gradients of temperature and or water vapor
in the atmosphere bend microwave rays up and down (ducting) which can cause
interception of the beam by the ground (Hunter, 1996). Doppler
radar uses an algorithm filter to eliminate most of the ground clutter
(Burgess and Ray, 1992).
A commonly discussed limiting factor is the effect
of distance from the radar on the accuracy. The Earth's curvature
and standard refraction force the beam to be elevated above the surface
with increasing range (Figure
1.1) (Brown and Wood, 1987). Due to beam overshoot the radar
does not sample layers near the surface. This will be more pronounced
in the cool season when the cloud bases are lower (Hunter, 1996).
Beam undershoot can be a problem close to the radar. This may cause
a "cone of silence" region surrounding the radar where precipitation is
underestimated (Cammarata, 1998). The cone of silence region is usually
within 8 miles of the radar site.
1.3.3 Rain Gauge Measurement
Despite radar advancements, rainfall estimates are
usually based on point observations of rainfall from gauge data.
The rain gauge's long service and widespread use has made it the standard
for measuring surface rainfall (Hunter, 1996). However, there
is error in gauge measurement especially due to turbulence and wind flow
losses (Yang et al., 1998). Wilson and Brandes (1979) determined
that wind/turbulence errors are usually around 5%, but with high winds
in thunderstorm outflows can be as high as 40%.
In general, gauge accuracy is high. The primary
problem is that the gauge measurement is for a point, whereas, the radar
yields a rainfall estimate for a much larger area. Distances between
National Weather Service gauges can often exceed 60 miles. Estimating
or interpolating precipitation events from these scattered gauge observations
can misrepresent the event, especially convective showers and even large-scale
stratiform precipitation events. The WSR-88D radar certainly has
an advantage in providing a surface precipitation estimate because of the
high spatial and temporal resolution
.
1.3.4 Interpolation Techniques
The WSR-88D radar 4 km by 4 km grids are composed
of range bins. The radar corrects isolated reflectivities and normalizes
the bin reflectivity data (Figure
1.2) before the Z-R conversion is performed and summarized for the
grid. Since it would be costly and impractical to have a rain gauge
for each bin, an interpolation technique is needed to estimate precipitation
where there are no rain gauges. This study used two interpolation
techniques to create a precipitation surface: inverse distance weighting
(IDW) and kriging.
The inverse distance weighted interpolator (IDW)
assumes that each data point has an influence that diminishes with distance.
Cells closer to the processing cell gets weighted higher than those farther
away (ArcView Spatial Analyst, 1996). One advantage to IDW is the
faster performance speed, but it has a tendency to create a pattern of
concentric contours around the data points (Surfer for Windows, 1996).
The interpolated values are also bounded by the minimum and maximum values
of the analysis data. This is a disadvantage because in order for
the interpolated surface to be representative it should predict locations
of maximum and minimum values even when they are not included as original
sample points (Lam, 1983).
One of the most flexible interpolation schemes is
kriging. Kriging develops variograms that show the correlation between
the base and surrounding stations as a function of distance (Young, 1992).
These variograms are used to determine weights given to the surrounding
station values (Surfer for Windows, 1996). There are two systems
of kriging procedures, simple kriging and universal kriging.
Lam (1983) provides a thorough analysis as well as calculations from the
two kriging methods.
Universal kriging was used for this analysis because
it has less restrictive assumptions about the data being used and because
of precipitation's nonstationarity over space. The stationarity assumption
requires that all sample points are taken randomly and independently from
one simple probability density function (Lam, 1983). Universal kriging
assumes that the increments of the variable have some properties of stationarity
only within a neighborhood and that the trend or drift for a neighborhood
can be described by a polynomial function (Lam, 1983). Drift is defined
as a systematic change in the data at a particular location (Arc/INFO,
1996).
A major advantage of either kriging method is that
it can be used on almost any data set (Surfer for Windows, 1996).
Since kriging is based on the regionalized variable theory, statistical
inferences about the data are utilized for the modeling (ARC/INFO, 1996).
The primary downside of kriging is the computations can be slow for larger
data sets (Surfer for Windows, 1996).
Determining the most accurate interpolation technique
was mandatory since the interpolated surface would represent the actual
rainfall for the analysis. No interpolation technique is superior
to all others for all applications. Therefore, this study utilized
two theoretically different interpolation techniques in order to provide
the most accurate precipitation surface.
A rainfall accumulation comparison study was conducted using the Columbia National Weather Service WSR-88D rainfall estimates and rain gauge data from a network of densely-spaced rain gauges (Figure1.3). The recent installation of the radars, the paucity of research evaluating WSR-88D precipitation estimates, and the difficulty of applying results from different regions demands such a comparison. The evaluation was carried out using a Geographical Information System (GIS) and statistical models. Chapter 2 follows with a more detailed explanation of the methodology of the study and a description of the study area, time period, and data. Chapter 3 contains results of the GIS and statistical analysis. Chapter 4 provides a discussion of the results and the final chapter contains a brief summary of the study and a discussion of future research potential.
2.1 Spatial and Temporal Characteristics
of the Research
Rainfall estimates from the Columbia National Weather
Service WSR-88D radar were compared to rain gauge data from a network of
72 densely-spaced rain gauges. The gauges were installed and maintained
in Lexington County, South Carolina, by the Lexington County Department
of Planning and Development and the South Carolina State Climatology Office.
The WSR-88D radar is within the county, providing a range to the gauges
that decreases the potential for error due to beam elevation. The
rain gauge network consists of 62 manually read and 10 automated recording
gauges placed at a density of approximately 1 gauge per 10 square miles.
Rain gauge and radar estimates for 7 storms, covering a variety of synoptic
types and precipitation patterns during 1997-1998, provide a basis for
detailed comparison.
2.2.1 Precipitation Events
Gauge accuracy, availability and accuracy of radar data, and synoptic type influenced the choice of 7 precipitation events. Three stratiform systems, 3 convective events, and 1 tropical precipitation episode were selected (Table 2.1). The original data set included 2 additional events, March 18-19, 1998 and June 2, 1998, that had to be excluded because there was no radar data available throughout several hours of each event. Hourly data from the tipping gauges confirmed that moderate rainfall was falling during these missing hours. The availability and the accuracy of the radar data was the single most limiting factor in selecting the events.
2.2.2 WSR-88D Estimated Precipitation Data
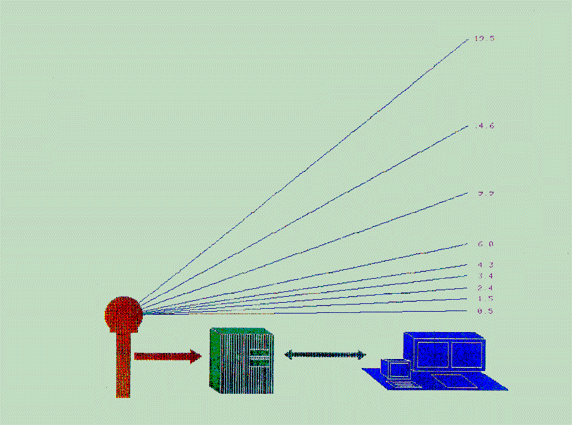
The primary product of interest for this study is
the precipitation estimation products from the WSR-88D radar. The
radar does not record precipitation directly instead it processes a returned
reflectivity from the precipitation droplets in the volume of the radar
beam. (The following discussion about the radar was acquired
and summarized from the WSR-88D Training Manual.) The precipitation
preprocessing algorithm uses base reflectivity data from the four lowest
elevation angles as input (regardless of the VCP). The base reflectivity
is quality controlled in order to get the best reflectivity values to build
a sectorized hybrid scan (1 o * 0.54 nautical mile sample volume).
The hybrid scan is constructed such that the best possible reflectivity
value from the lowest four tilts is selected for conversion to rainfall
rate. From the hybrid scan, reflectivity data (dBZ) is converted
to rainfall rate using the Z-R relationship (Z=300R1.4 is the default relationship).
The rainfall rates at the 0.54 nautical mile (nm) * 1o resolution
are then converted to a new resolution, 1.1 nm * 1o. This is achieved
by averaging the rates in the adjacent 0.54 nm gates, and placing the average
in the corresponding 1.1 nm gate. Throughout this entire process
various quality control checks are performed such as the example in Figure
1.2. The precipitation accumulation algorithm is then implemented
to produce scan to scan and hourly accumulation products. The one
hour digital precipitation array (DPA), an accumulation in the 1.1 nm *
10 polar form converted to a 2.2 *2.2 nm rectangular grid, was retrieved
for this study.
Once the data is recorded at the National Weather
Service a NEXRAD Information Dissemination Service (NIDS) vendor distributes
the products to the various users. The binary data from the NIDS
vendor was ingested at the South Carolina State Climatology Office for
the study period. A C program from the University of South Carolina
was utilized to decode the binary code and provide a tabular output (Appendix
2.1). This data was then entered into a Geographic Information System
which will be discussed in section 2.3.1.
Bad WSR-88D grid values were summarized using the
University of South Carolina program. An hourly analysis of each
event uncovered that the bad grid values were only an indication that the
radar was in "clear air mode". These bad grid values were set to
0 (inches) precipitation since the "clear air mode" indicates no precipitation
was observed.
Events were excluded from the study when the radar
was temporarily in-operational or if the radar was switched to "clear air
mode" before the entire precipitation event was concluded. The later
occurred more frequently since the NWS radar operators do not leave the
radar in precipitation mode unless necessary because of stress on the system.
The radar has to perform an increased frequency of scans at more elevations
during the precipitation mode. The operators sometimes switch the
radar to "clear air mode" as the precipitation event is ending, however,
the region may still be receiving as much as 0.10 inches (Charnick, 1999).
2.2.3 Manual and Automated Gauges
Through collaborative efforts, the Lexington
County Department of Planning and Development and the South Carolina State
Climatology Office installed 109 manual daily recording gauges and 10 automated
hourly rain gauges in Lexington County, South Carolina. The manual
gauges were National Weather Service approved 4 inch diameter by 14 inch
height plastic rain gauges. The automated gauges were tipping buckets
that record at 15 minute intervals. The network of gauges was placed
throughout Lexington County in order to provide a dense coverage that would
serve as the true and accurate base precipitation coverage for the radar
comparison study.
Since the study period extended over 2 years, numerous
rain gauge volunteers did not record all precipitation episodes.
A detailed daily quality control check on all the data also revealed the
variation in data quality. This process led to the elimination of
those gauges that had excessively high or low precipitation values, combined
events, or missing days. Three National Weather Service Daily Cooperative
Stations in the county - Batesburg, Pelion, and Gaston - were added to
the study because of the consistency between reporting techniques.
Table 2.2 provides the number of gauges reporting during each event.
Only stations reporting at least 5 out of the 7 events were utilized in
the analysis.
The 10 automated tipping gauges were installed within
2 river basins, Twelve Mile Creek and Fourteen Mile Creek (Figure
2.3). For equipment consistency with other hydrological studies
being conducted, the UNIDATA Model 6506B tipping bucket was selected for
this study. Figure
2.1 provides details about the tipping gauges such as calibration and
recording sensitivity. These 10 gauges were analyzed separately to
prevent introducing error due to different recording techniques.
The study of the 2 connected basins provided a smaller scale analysis that
included hourly and daily recording intervals.
2.2.4 Inverse Distance Weighting and Kriging
The point data from the network of rain gauges was
used to create an interpolated precipitation surface. The interpolation
was performed by kriging and IDW. IDW was carried out in ArcView
Spatial Analyst. An Avenue script (ESRI programming language) executed
the kriging interpolation (Appendix 2.2).
The accuracy of each interpolation scheme was measured
for each event by using half of the data to interpolate and comparing interpolated
values against data from the other half of the set. The IDW and kriging
surface were each subtracted from actual values yielding an interpolation
error. An Analysis of Variance (ANOVA) statistical test determined
if the technique errors were significantly different (Appendix 2.3).
The range of the error as well as the absolute value of the summed error
was also considered. The interpolation technique with the smallest
range and lowest absolute error per event was used to interpolate a surface
for the entire network of stations. The most accurate technique was
also used to create a precipitation surface from the tipping gauges for
the 2 basins.
2.3 Radar and Gauge Comparison
The purpose of the study was to explain quantitatively any discrepancies between the gauge and radar rainfall amounts. The project used a loose coupled Geographic Information Systems (GIS) approach to model the relationship between the gauge and radar data. A Geographic Information System (GIS) was developed to analyze, by storm event, the discrepancies between the gauge and radar data. GIS provided the platform needed to manipulate the layered, spatially distributed databases involved in the study. Figure 2.2 provides a conceptual model of the analysis.
2.3.1 Geographic Information System
The GIS software used for this study was ArcView
and its programming language Avenue. The modeling applications were
implemented using local, focal, and zonal operators (Tomlin, 1990).
Loose coupling between GIS and the Statistical Analysis Software (SAS)
was also required. The embedded applications were developed
through the ArcView scripting language - Avenue.
The GIS was used to develop a spatial database of
the radar and gauge precipitation estimations. The GIS was used to
separate Lexington County into zones to determine if the accuracy of doppler
derived precipitation was consistent spatially. The zone separation
boundary was 8 miles from the radar site based on the radar cone of silence
influence (Cammarata, 1998). Local operators were used to calculate
the difference between the radar estimates and the interpolated gauge surface.
An embedded script was developed to calculate the root mean square error
(Appendix 2.4) for each event. The root mean square error is a method
for measuring the model performance by summarizing the mean squared error.
RMSE is calculated by:
RMSE = [N-12]0.5
where
Ri is the radar estimated precipitation for observation i
Gi is observed precipitation from gauge data
N is number of WSR-88D grid cells
Arcview zonal operators were used to calculate zonal statistics for the county-wide zone as well as the 2 zones that separated the county according to distance from radar. An embedded script was created to summarize the interpolated gauge data and difference data by the WSR-88D grid boundaries (Appendix 2.5). This function was necessary in order to convert the interpolated point data into a comparable block of data that could be compared to the WSR-88D 4 km by 4 km grids. Arcview zonal operators performed the zonal statistics for the WSR-88D grids. The mean of the interpolated surface for each WSR-88D grid was calculated and displayed. This assisted in the visual comparison of the data as well as the SAS analysis.
2.3.2 Loose Coupled Statistical Model
A loose coupled model between the GIS and SAS was
invoked to perform a regression model to estimate the degree of closeness
of the relationship between the radar and gauge precipitation estimates
(Appendix 2.6). Before the regression could be performed the distribution
of WSR-88D and gauge data were examined. Since neither gauge nor
doppler data were normally distributed a logarithmic transformation was
required before the regression analysis could be implemented. TableCurve
2D software (SPSS, 1995) was used to test whether the relationship between
log transformed gauge and radar data was linear.
SAS was also used to calculate the Analysis of Variance
(ANOVA) on the radar-gauge differences represented as percentages to determine
if any of the 7 events were significantly different from each other.
The WSR-88D data was divided by the gauge data using an embedded GIS function.
This yielded a percentage value that was evaluated by a SAS ANOVA test
(Appendix 2.7). The percentage data was used since the scale of the
7 different precipitation events varied by as much as 5 inches. Percentage
data put all the events into a comparable scale. A logarithmic transformation
on the percent data was performed before the analysis began since this
data also failed the test for normality. The Student-Newman-Keuls
(SNK) model tested the homogeneity of all the event means.
2.3.3 Radar and Tipping Gauge Analysis
The same GIS and statistical models as discussed above were performed for the radar and tipping gauge comparison. The 10 tipping gauges and the 22 WSR-88D Grids within the basin were compared using the embedded GIS applications as well as the SAS regression and ANOVA models. This basin was analyzed separately to provide a smaller scale study. The study was also separated to avoid introducing potential error caused by combining tipping gauge measuring techniques with the standard manual measuring methods into one analysis. Having the smaller basin output using the tipping gauge interpolated surface as the rainfall "ground truth" enhanced the results for the original manual gauge study.
2.3.4 Synoptic Classification and Influence
The final phase of the project was to determine the potential synoptic or inherent factors causing the discrepancies between the radar and gauge data. Daily meteorological surface charts and National Weather Service "Summary of the Day Weather Analysis" (Figure 2.3) were used to identify the synoptic situations for each event. A number of physical factors influence the relation between measured radar reflectivity and surface rainfall. Typical factors include significant growth of raindrops by accretion within 1.2 miles of the surface, evaporation at lower levels, presence of strong vertical air motions and hailstones in convective storms, and large vertical gradients of temperature and or water vapor in the atmosphere. Understanding and identifying these factors are crucial if researchers are ever going to make the best estimate of rainfall from the radar or gauge network.
This summary of results begins with the outcome of the interpolation validation. This validation was a significant part of the research's foundation and an inaccurate precipitation surface would manifest itself throughout the analysis prohibiting a true radar-gauge comparison. The majority of the chapter will include the results of the Geographic Information System and statistical models.
3.1 Interpolation Validation and Estimation
The ANOVA showed that there was no significant difference between IDW and kriging for any of the 7 events. Therefore, the technique with the lowest summed absolute error and/or smallest error range was used for the interpolation of the base gauge data. Table 3.1 summarizes the results.
Altogether in the 7 storms, 1,099 (157 WSR-88D Grids
* 7) individual radar-gauge comparisons were made. The total amount
of rain involved varied considerably from storm to storm, from gauges recording
an average of 6.3 inches on September 3-4, 1998 to gauges recording an
average of 0.9 inches on August 9, 1998 (Table 3.2). When all the
storms were combined, agreement between gauges and radar was weak, with
the total for the gauges being 20.9 inches on average and that for the
radar 8.1 inches on average, a difference of 61%. However, when the
storms were considered individually two storms had a radar-gauge difference
less that 5%.
The following sections will attempt to explain differences
between radar and gauge precipitation in each storm. The SPSS linear
test proved that using a non-linear equation function did not improve the
relationship between the doppler and gauge data, therefore, the results
of the SAS linear regression model was documented for all events.
Table 3.3 and Table 3.4 summarize the results of the root mean square error (RMSE)
and the SAS regression model for all 7 events for the county zone, the
8 mile cone of silence zone and the zone outside the 8 mile cone of silence
boundary. Figure
3.1 displays the zones. Table 3.5 provides the RMSE and the regression
output for the Twelve Mile Creek and Fourteen Mile Creek (creek basin)
tipping gauge comparison.
These sections will also include an explanation
of the physical synoptic factors attributing to the differences.
The storms are grouped by synoptic type; stratiform, convective, and tropical,
for discussion purposes. It is difficult to draw solid conclusion
based solely on synoptic type since this analysis is limited to 7 events.
3.2.1 Stratiform Events
Three events were classified as stratiform in nature;
September 24-28, 1997, January 22-23, 1998, and February 3-5, 1998.
In warm frontal storms, large-scale lifting or overrunning creates extensive
areas of clouds and precipitation. The precipitation is generally
stratiform in nature with rain often persisting for hours. The precipitation
is usually uniform, but can have mesoscale bands of heavier rain.
In all 3 events the hourly rainfall was generally light and the drops were
small as indicated by observation comments from the observers. Most
of the light, drizzle rain was not detected at all. Even during the
hours when the rainfall was moderate, the raindrops were apparently smaller
than average causing the radar to seriously underestimated the rain.
The radar performed the worst out of all 7 events
during September 24-28, 1997. Figure
3.2 and Figure3.3
shows the difference between WSR-88D estimated precipitation and the gauge
precipitation. (Note: The histograms throughout this study show differences
at a scale of 100m by 100m not at the 4 km by 4 km resolution. The
original interpolated surface was at this resolution before being summed
by the 4 km by 4 km WSR-88D grids.) Most of the WSR-88D grids were
underestimated by -4.02 to -5.69 inches. The WSR-88D estimated
precipitation averaged only 16% of the gauge recorded precipitation.
Figure
3.4 and Figure
3.5 displays the comparison between the tipping gauge data and the
WSR-88D surface. The underestimated results were consistent for this
smaller scale analysis. These 22 WSR-88D grids were off by -3.5 to
-6.5 inches.
The RMSE for the September 24-28, 1997
storm was 4.31 inches for the entire county, 4.15 inches outside the 8
mile cone of silence region, 4.92 within the cone of silence region, and
4.90 inches in the Twelve Mile Creek and Fourteen Mile Creek basin.
The R2 confirms the weak relationship between the radar and gauge precipitation
amounts (Table 3.4 and Table 3.5). The F statistic for the overall model
is not significant, indicating that the WSR-88D grids do not explain a
significant portion of the variation in the gauge data. The R2 of
0.27 with a F statistic of 7.551 for the creek basin proved to be significant.
One aspect of this event which should be considered
is that the Columbia radar underwent a calibration change in mid-October
after this event occurred. The calibration was suppose to improve
the radar's estimation capabilities. This event was included to serve
as a control to see if significant improvement was noticed after the calibration.
Results from the January 22-23, 1998, did not substantially
improve. The WSR-88D estimated precipitation averaged a low 26% of
the gauge precipitation. Figure
3.6 and Figure
3.7 show gauge and radar estimates and the differences between them.
The histogram in Figure
3.7 shows the majority of the grid cells were underestimated by -0.86
to -1.04 inches. The tipping gauge analysis enforces this conclusion
(Figure
3.8 and Figure
3.9). Table 3.3 and Table 3.5 shows the RMSE values. The R2 of
0.52 for the entire county, 0.66 for cone of silence region, and 0.57 outside
cone of silence was surprisingly high. The spatial precipitation
distribution displayed in Figure
3.6 does not visually support this moderate correlation.
The February 3-5, 1998 WSR-88D estimated precipitation
was consistently low as compared to the gauge data. The WSR-88D estimated
precipitation averaged 24% of the gauge precipitation with two WSR-88D
grids recording less than 10% of that by the gauges. Figure
3.10 and Figure
3.11 exhibits this weak relationship between the WSR-88D and the gauges.
The WSR-88D grids within the creek basin were underestimated by at least
-2.26 inches (Figure
3.12 and Figure
3.13). The 0.91 RMSE only varied by 0.01 within and outside the
cone of silence. There was no correlation between the radar and gauges
within the cone of silence region. Outside the cone of silence the
relationship was weak with an R2 of 0.27.
In summary, it appears that in stratiform storms
with light, widespread rain and small dropsize there is significant underestimation
by the radar. Even excluding the September 1997 storm because of
the calibration change, the January and February storms were underestimated
by 75%.
3.2.2 Convective Storms
Three events were classified as convective storms;
October 22-26, 1997, April 8-9, 1998, and August 9, 1998. April 8-9,
1998 included a prefrontal squall line and hail reported on both days.
Considering these hail events and the typically large dropsizes during
convective storms, the radar was expected to overestimate the events, especially
the April storms.
It is surprising then, that precipitation during the October
event was underestimated by the radar. The highest WSR-88D
grid precipitation amount was only 63 % of the gauge data. Figure
3.14, Figure
3.15,Figure
3.16, and Figure
3.17 provides the radar-gauge comparison. Despite the overall
low estimation, an R2 of 0.30 was found for the zone outside the cone of
silence and an R2 of 0.48 in the creek basin (Table 3.4 and Table 3.5).
This demonstrated that the patterns and distributions of the rainfall event
were somewhat related. The F statistic was found to be significant
in both cases. The significance of the F statistic for the cone of
silence was probably attributed to the large number of observations (123).
The April and August events had the highest average
percent accuracy with the radar estimating 96% of the gauge data.
The radar estimation accuracy was not consistent for either event.
In several grids, the radar estimated only 17% of the gauge data
during the April storm while others were estimated at 210% of the gauge
data. The gross overestimation could be related to hail. NWS
storm reports documented hail in Lexington County on April 8th. Sixty-six
WSR-88D grids were overestimated and 91 underestimated. Figure
3.18, Figure
3.19,Figure
3.20, and Figure
3.21 presents the radar-gauge relationship for the county and the creek
basin. There was only a 0.05 inch difference between the inside and
outside cone of silence regions, 0.53 and 0.58 respectively. Despite
the improvement in the radar estimation the R2 was 0 for the county because
grid for grid the correlations were weak.
Similar results were found for the August storm.
Radar estimates in several WSR-88D grids were only 5% of the gauge
data while others were 481% of the gauge data. There may have been
hail during this event even though none was officially reported and this
could account for the outrageous overestimation. The extreme overestimation
could also be a result of the point gauge measurements missing cells with
embedded heavy rain. Even with a dense network of gauges these heavy
rain cells can be missed unless the event is occurring at the exact gauge
sites. Fifty-four WSR-88D grids were overestimated and 103 underestimated.
Thirteen grids were overestimated by 100% to 181% of the gauge data. Figure
3.22, Figure
3.23,Figure
3.24, and Figure
3.25 displays the radar-gauge relationship for the county and the creek
basin. The grid for grid correlation was also weak for the August
storm with an R2 of 0 for all zones. The RMSE ranged from 0.49 to
0.75 (Table 3.3 and Table3.5).
In an effort to explain the extreme overestimation
for both the April and August event Figure
3.26 was created to display the WSR-88D grids associated with the extreme
overestimation. Several of the cells are consistent among both events.
It may be coincidental since the April grids match where there were reports
of hail. Those grids within the 8 mile zone may be related to the
distance from radar factor.
It is also worth suggesting that there could be
an association among the grids due to proximity to Lake Murray. There
are two potential scenarios. A discontinuity between the moisture
and temperature levels over the land and the water exists. The land
will be warmer than the water in the afternoon creating a lake to land
breeze which could cause a rainshadow immediately near the lake with rain
being produced along a boundary away from the lake. The radar may
not detect the boundary and therefore overestimate the precipitation close
to the lake.
Scenario two is more appealing in these two events.
The thunderstorms may be picking up moisture as they move over the lake
dropping it at a distance away from the lake. The radar would detect
the increased moisture in the atmosphere near the lake and record a heavier
rainfall than is actually occurring while the heavier rain is actually
being deposited a distance away with the radar underestimating the amounts
in these locations. It is impossible with only 2 events to
draw any concrete conclusions.
In summary, the factors during these convective
storms which probably have the greatest effect on radar measurements is
enhancement of reflectivity by hail and larger than average raindrops and
diminution of estimation by small drops and downdrafts. The reflectivity
from hail and large droplets are high as compared to the precipitation
equivalent. Conversely, smaller drops yield a lower reflectivity
as compared to the precipitation equivalent. The influence of downdrafts
could also be causing the radar's underestimation of precipitation because
downdrafts are associated with the rainshafts in convective cells.
Austin (1986) found that downdrafts can cause a 15% to 50% underestimation.
3.2.3 Tropical System Event
Fortunately for South Carolinians, only 1 tropical
system significantly impacted the study area during the period September
1997 - September 1998. This is a limiting factor for this section
because only one example can be provided. The remnants of Tropical
Storm Earl moved across South Carolina on September 3-4, 1998. This
system produced heavy rains exceeding 5 inches within a 25 hour period.
The NWS anticipated the radar's problem with handling this tropical event
so the alternate Z-R relationship (Z=250R1.2) was implemented. The
NWS staff emphasized that the radar's performance definitely improved in
comparison to the performance during Tropical System Danny, July 1997.
Despite this suggested improvement the radar consistently
underestimated the event. The WSR-88D estimated precipitation ranged
from 20% to 86% as compared to the gauges. Table 3.2 shows that the
highest WSR-88D grid estimate of 4.94 inches was the lowest value indicated
by the gauges. Figure
3.27, Figure
3.28,Figure
3.29, and Figure
3.30 presents the radar-gauge comparison spatially. The majority
of the 100m by 100m grid cells were underestimated by -2.94 to -3.67 inches.
The results from the tipping gauge comparisons show similar results.
The RMSE varied from 2.36 inches within the cone of silence region to 3.38
inches outside the region (Table 3.3 and Table 3.5). The R2 values for
the two zones within the county were 0.03 (Table 3.4). The R2 for
the creek basin was 0.87 with a significant F statistic of 132.409.
This would indicate that within the creek basin the WSR-88D grids explained
a significant portion of the variation in the gauge data. Since this
is the only event where the creek basin R2 was substantially higher than
the manual gauge study it is impossible to conclude that it was anything
other than a random occurrence.
The factor's influencing the radar's ability to
estimate precipitation during the passage of tropical storms is similar
to that experienced during any system that consists of tropical maritime
conditions. This is not a rare event in South Carolina. During
tropical maritime conditions there is an abundance of moisture that makes
it difficult for the radar to determine a representative reflectivity.
These systems also have embedded thunderstorms with overestimation due
to larger dropsizes in some areas and underestimation in others due to
the presence of strong downdrafts. Throughout history radars have
had difficulty handling tropical systems (Brown, 1999)
3.3 Relationship Between Radar-Gauge Differences for Seven Events
In an attempt to determine the relationship between
the 7 events, the WSR-88D precipitation represented as a percentage of
the gauge data (1, 099 observations) was entered into an ANOVA to test
if the events were significantly different. The Student-Newman-Keuls
(SNK) tested the homogeneity of all the means. The percentage data
was used since the scale of the 7 different precipitation events varied
by as much as 5 inches. Figure
3.31 presents the results.
There was not a significant difference between the
event means for October 22-26, 1997, January 22-23, 1998, and February
3-5, 1998. However, the other four events were each significantly
different. The results did not coincide with the synoptic classification
factors discussed earlier, however, the January and February storms were
both stratiform events. One consistency between October 1997, January
1998, and February 1998, was that the radar's performance was weakest during
these events excluding the September 1997 storm because of the calibration
change. It is not surprising that the means were different based
on the varying percent of accuracy levels as well as the spatial distribution
of the results.
The results of the Geographic Information System (GIS) and the SAS regression and ANOVA models are generally consistent in their analysis of the radar-gauge comparison. Both show that the radar usually underestimates precipitation independent of the storm type. This chapter briefly discusses the utility of the loose coupled GIS model, followed by a more thorough discussion of the radar's performance.
4.1 Utility of the Loosed Coupled GIS
GIS provided the platform needed to manipulate the layered, spatially distributed databases involved in this study and the specific GIS model created for this study provided an effective and efficient tool for examining the relationship between the radar and gauge data. The ability to query, chart, map, summarize, and tabulate output within one model was invaluable for the process.
4.1.1 Reliability of the ANOVA and Regression models
The model would have been more temporally efficient had the ANOVA and regression model been embedded within the GIS as had the RMSE computations. The alternative loose coupled approach was used since ArcView software performed the analysis at the finest resolution of the interpolated surface (100 m * 100m). This resolution was inappropriate because it was not compatible with the radar output. In addition, the total number of small grids (384,400) distorts interpretation of the regression results due to the large number of degrees of freedom. As with any statistical computation, the individual tests should not be used as a stand-alone model of the event.
4.2 Radar Rainfall Error Sources
The radar consistently underestimated precipitation in 5 out of the 7 storms studied. The radar also underestimated precipitation in the April and August storms, but some grids were excessively overestimated. The potential physical factors causing these errors were provided in Chapter 3. The discussion that follows will explain why these factors influence and diminish the radar's performance.
4.2.1 Reflectivity Estimate
The WSR-88D radar provides more sensitive and reliable
reflectivity estimates than previous radars. However, there are still
limitations due to the inherent use of the radar to estimate precipitation.
Radars can't directly measure rainfall, nor can they directly measure reflectivity,
Z. Reflectivity is dependent on dropsize distribution, but the radar
can't measure dropsize distribution. Radars estimate Z from returned
power. The estimation of reflectivity is calculated by:
Ze = Pr R2
____
C
where Pr = returned power
R = range
C = radar constant
The radar's inability to measure dropsize distribution has historically
been recognized as a problem since different dropsize distributions can
generate identical reflectivities, affecting the accuracy of the rainfall
estimate. For example, a cubic meter of the atmosphere with 729 drops,
each with a diameter of 1mm, falling at 4 m/s yield the same reflectivity
as a cubic meter of the atmosphere with one drop 3mm in diameter falling
at 7 m/s. The actual rainfall rate differs between 0.22 inches/hr
for the 729 drops to 0.01 inches/hr for the one drop (WSR-88 D Training
Manual, 1993). This error source may have been a significant factor
in the Lexington County study. The stratiform events were underestimated
because of small dropsize, while grids within the convective events were
overestimated because of larger dropsize.
The reflectivity estimate may also be contaminated
by ground clutter, anomalous propagation, hail, and partial beam filling.
Hail is probably the only other potential reflectivity error source occurring
within this study. Similar to the impact of large dropsizes hail
causes a large reflectivity compared to the precipitation equivalent.
4.2.2 Z-R Relationship
In addition to the reflectivity error sources we
must consider the error in the conversion from the reflectivity (Z) to
the rainfall rate (R). There is no unique Z - R relationship.
Conversion from reflectivity to rainfall rate is accomplished using
Z=300R1.4 (Burgess and Ray, 1992) although an alternative equation
Z=250R1.2 (Cammarata, 1998) may be used during tropical events with special
permission of the WSR-88D Operational Support Facility (OSF) in Norman,
Oklahoma (Burgess and Ray, 1992). Another potential relationship
that can be used for intense convective cells is Z=400R1.3 (Austin, 1987),
however, most forecast offices including Columbia do not implement this
formula.
A single Z-R relationship is inadequate to provide
the appropriate conversion for all precipitation events. During this
study, the default Z-R relationship was used in 6 of the 7 events.
As documented, the Columbia radar operators switched to the alternate Z-R
relationship during Tropical System Earl's passage. The Columbia
NWS staff suggested that the radar's performance was improved by using
the Z=250R1.2 (Cammarata, 1998), however, results from this project show
a substantial underestimation by the radar. For the other 6 events,
the use of one Z-R relationship was probably an error source.
4.2.3 Distance from Radar
Since the study area was within 40 miles of the radar site beam, overshoot was not a potential error source. Beam undershoot was expected to be a problem within approximately 8 miles of the radar site. The results of this analysis didn't find a consistent, pronounced underestimation in the "cone of silence region". The "cone of silence" RMSE was actually less in three storms as compared to the RMSE outside the 8 mile boundary. It has been suggested that the entire study area of Lexington County is in the cone of silence region. Results from this project discount this theory since there is not an improvement in the radar's performance along the outer grids of the county.
4.2.4 WSR-88 D Calibration
A potential error source as documented by the WSR-88D
Training Manual (1993) is incorrect hardware calibration that would impact
the Z estimation. This is introduced outside the Z estimation section
because it differs from the other error sources. The WSR-88D is self-calibrating
and therefore improved over previous radars. However, the radar does
require calibration such as performed on the Columbia radar in mid-October
1997. I introduce incorrect calibration as a potential error source
for the Columbia radar.
Reports such as that by Lott and Sittel (1993) present
varying levels of performance for radars within one region.
These radars experience the same error sources of reflectivity. They
use the same default Z-R relationship and yet the performance for several
of the radars were significantly better than that of others. Could
the error source be incorrect hardware calibration? The answer is
beyond the scope of this project.
The final phase of the project was the test for homogeneity
between the 7 events. If consistency had existed, a potential constant
coefficient of adjustment could have been combined with the radar data
to make the surface more comparable to the gauge results. This was
an ideal, but unrealistic expectation considering the varying performance
levels of the radar.
The purpose of this project was to determine the accuracy of the WSR-88D radar rainfall estimates as compared to precipitation measured in a dense rain gauge network. The study explained, quantitatively, the discrepancies between the gauge and radar rainfall amounts for seven precipitation events in Lexington County, South Carolina. The project used a loose coupled Geographic Information Systems (GIS) approach to model the relationship between the gauge and radar data.
The results show that the radar consistently underestimated
precipitation in most circumstances. The radar was unable to accurately
estimate precipitation regardless of synoptic type. It overestimated
rainfall in individual grid cells during 2 events, but the majority of
the WSR-88D grids within these storms were underestimated. The mid-October
1997 calibration did improve the radar's performance as compared to September
24-28, 1997 event.
The results from the tipping gauge comparison echo
the results from the manual gauge study. The magnitude of error between
the radar and the gauge was similar regardless of which recording equipment
was used, tipping or manual. Having the ability to compare the radar
with two different ground recording devices strengthened the results.
Error sources such as varying dropsizes and strong downdrafts were provided as physical factors altering the radar's performance. Beam undershoot associated with being within 8 miles of the radar did not influence the radar's estimation capabilities. This conclusion may be skewed by the overall weak performance of the radar. The question of incorrect hardware calibration was also suggested as an error source.
5.3 Gauge and Interpolated Techniques
The network of 62 manual and 10 tipping gauges placed at a density of approximately one gauge per 10 square miles provided the dense spatial coverage needed to accurately represent the rainfall across an extended area. A continuous precipitation surface was required for the radar-gauge comparison. Any error in the interpolated gauge surface would have propagated through the radar-gauge comparison introducing a bias into the results. The interpolation error in this study was decreased due to the dense station coverage and by choosing the more accurate of the two interpolation techniques for each event.
5.4 Expectations of Decision-Makers and the Research Community
Most climatological studies do not have access to a dense network of reporting stations. Researchers depend on data from the sparse network of National Weather Service stations. Ironically, the research community and decision makers were hopeful that the WSR-88D would provide the continuous precipitation surface. The results from this study conclude the radar can not yet provide the spatial distribution of surface rainfall that is needed for the many operational and research applications.
5.5 Real-Time Calibration With Automated Gauges
I think that beyond the potential error sources discussed in this study there is one very important aspect of the radar's operation that is being omitted and may be the missing link that will significantly improve the radar's performance. As documented by the WSR-88D Training Manual (1993), the use of real-time automated rain gauges for calibration was a major reason the radar rainfall error sources were expected to be minimized in the WSR-88D. The comparison to a network of automated rain gauges was suppose to be performed to reduce the Z-R relationship errors and effects below the beam. This comparison was expected to take place before the precipitation products were built. This final very important stage has not been implemented and there are questions as to whether it will ever be employed.
Because of the great variability in the intensity
and distribution of precipitation, more radar-gauge comparisons should
be conducted to cover a larger number of storms. This study was purposely
limited to precipitation falling within 40 miles of the radar site, however,
the Columbia radar provides a coverage for the majority of South Carolina.
An analysis of the radar's performance statewide is needed. Even
though a dense network of stations statewide is impracticable, use of the
National Weather Service Cooperative network supplemented with data from
the State Climatology Office's automated gauges and volunteer weather observers
could provide enough stations for a general overview analysis.
Stimulated by the results of this study, the State
Climatology Office (SCO) has already embarked on an extension to the project
that would include analysis of the radar level II base reflectivity data.
This base reflectivity data will be examined for the same 7 events in an
effort to conclude whether the error sources were caused by inaccurate
reflectivity values, an incorrect Z-R conversion, or a combination of the
two. The base reflectivity data will be entered into different Z-R
equations in an effort to produce a more reliable radar estimate of precipitation.
The precipitation amounts will then be calibrated using the network of
gauges. The resultant product should provide a much improved estimate
of precipitation.
Radar-Rainfall Estimation Uncertainty. Proceedings of the American Meteorological
Society 13th Conference on
Hydrology. 133-36.
Anonymous Authors. 1996. Enhanced WSR-88D Radar-Rainfall Data Sets for Earth Science
Research. Proposal for
Funding. United States Department of Commerce.
Anonymous Author. 1998. Real-Time Calibration of Radar Precipitation Estimates. Unpublished Article. 1-36.
ARC/INFO Help Menu. 1996. Environmental Systems Research Institute Inc.
ArcView Spatial Analyst. 1996. Environmental Systems Research Institute, Inc.
Austin, 1987. Relationship Between Measured Radar Reflectivity and Surface Rainfall. Monthly Weather Review. 1053-70.
Badar, M.; Forbes, G.; Grant, J.; Lilley, R.; and Waters, A. Images in Weather Forecasting. 50-69.
Baker, S. 1999. Personal Communication.
Battan, L. 1976. Vertical Air Motions and the Z-R relation. Journal of Applied Meteorology. 15: 1120-21.
Brandes, E., and Wilson, J. 1988. Measuring Storm Rainfall by Radar and Rain
Gauge. Instruments and Techniques for
Thunderstorm Observation and Analysis. University of
Oklahoma Press, 171-186.
Borga, M.; Anagnostou, E.; and Krajewski, W. Propagation of Radar-Rainfall Estimation
Errors in Rainfall-Runoff
Modeling. Proceedings of the American Meteorological Society
13th Conference on Hydrology. J136-39.
Brown, M. 1999. Personal Communication.
Borwn, R., and Wood, V. 1987. A Guide For Interpreting Doppler Velocity Patterns. Use
and Interpretation of
WSR-88D WSR-88D Products By the Media. 1-44.
Burgess, D. W., and Ray, P. S. 1992. Principles of the Radar. Use and
Interpretation of WSR-88D WSR-88D Products by
the Media, Short Course. American Meteorological Society,
Boston
Cammarata, M. 1998. Personal Communication.
Charnick, R. 1999. Personal Communication.
Crum, T. D., and Alberty, R. L. 1993. The WSR-88D and the WSR-88D operational support
facility. Bulletin of the
American Meteorological Society 74: 1669-87.
Crum, T. D.; Alberty, R. L.; and Burgess, D. W. 1993. Recording, archiving, and using
WSR-88D data. Bulletin of
the American Meteorological Society 74: 645-49.
DeMers, M. 1997. Fundamentals of Geographic Information Systems. John Wiley & Sons, Inc.
Hunter, S. 1996. WSR-88D Radar Rainfall Estimation: Capabilities, Limitations and
Potential Improvements. National
Weather Digest. 20(4): 26-38.
Groisman, P.; and Legates, D. 1994. The Accuracy of United States Precipitation
Data. Bulletin of the American
Meteorological Society. 75(3): 215-27.
Joss, J., and Lee, R. 1995. The Application of Radar-Gauge Comparisons to
Operational Precipitation Profile Corrections.
Journal
of Applied Meteorology 34: 2612-30.
Klazura, G. E.1982. Differences Between Some Radar-Rainfall Estimation Procedures in a
High Rain Rate Gradient Storm.
Journal of Applied Meteorology 20(11):1376-80.
Krajewski, W.; Anagnostou, E.; and Ciach G. 1996. Effects of Radar Observation Process
on Inferred Rainfall Statistics.
Journal of Geophysical Research 101: 26,493-502.
Lam, N. 1983. Spatial Interpolation Methods: A Review. The American Cartographer. 10(2): 129-149.
Lott, N. and Sittel, M. 1996. A Comparison of WSR-88D Rainfall Estimates with recorded Amounts. National Climatic Data Center Technical Report 96-03.
Marsalek, J. 1981. Calibration of the Tipping-Bucket RainGage. Journal of Hydrology 53: 343-54.
Marshall, J., and Palmer, W. 1948. The distribution of rain drops with size. Journal of Meteorology 5: 165-66.
National Climatic Data Center’s Radar Resources. 1997. National Climatic Data Center Internet Site.
SAS/STAT User’s Guide. 1990. SAS Institute, Inc.
Seo, D.; Krajewski, W.; and Bowles, D. 1990. Stochastic Interpolation of Rainfall Data
from Rain Gages and Radar Using
Cokriging 1. Design Experiments. Water Resources Bulletin. 26(3):
469-77.
SURFER for Windows. 1996. Golden Software, Inc. Creating Grid Files. 5-14 – 38.
Tomlin, D. 1990. Geographic Information Systems and Cartographic Modeling. Prentice-Hall, Inc.
UNIDATA Equipment Manual. 1996. UNIDATA, Inc. Model 6506B Rain Gauge.
Wilmott, C. 1982. Some Comments on the Evaluation of Model Performance. Bulletin of American Meteorological Society. 63(11): 1309-1313.
Wilson, J., and Brandes, E. 1979. Radar Measurement of Rainfall - A
Summary. Bulletin of American Meteorological
Society. 60(9): 1048-58.
Wilson, W.; French, M.; Bhaskar, N.; and Anderson, R. 1997. Rain Gage and WSR-88D
Rainfall Accumulation
Comparison in Jefferson County, Kentucky. Proceedings
of the American Meteorological Society13th Conference
on Hydrology 111-12.
Woodley, W., and Herndon, A. 1970. A Raingauge Evaluation of the Miami
Reflectivity-Rainfall Rate Relation. Journal of
Applied Meteorology 14:909-28.
WSR-88D Operations Training Student Guide. 1993. United States Department of Commerce,
National Oceanic and
Atmospheric Administration, National Weather Service, Operations
Training Branch, Operational Support Branch.
Yang, D.; Goodison, B.; Metcalfe, J.; Golubev, V.; Bates, R.; Pangburn, T.; and Hanson,
C. 1998. Accuracy of NWS 8"
Standard Nonrecording Precipitation Gauge: Results and
Application of WMO Intercomparison. Journal of Atmospheric
and Oceanic Technology 15: 54-67.
Young, K. 1992. A Three-Way Model for Interpolating for Monthly Precipitation Values. Monthly
Weather Review 120:
2561-69.
Table 2.1 Seven Rainfall Events Examined in the Study
| RAINFALL EVENT | Synoptic Classification |
| Sept 24-28,1997 | Tropical moisture was pumped into the state by a low pressure system. Waves moving across frontal boundary. It was a stratiform precipitation event. |
| Oct 22-26,1997 | Cold front produced precipitation. Moist unstable air ahead of front sparked convective thunderstorms. |
| Jan 22-23, 1998 | The rain was caused by a warm front approaching from south and cold front from west. Had an inverted trough and cold air damming. Stratiform precipitation resulted. |
| Feb 3-5, 1998 | The low pressure in the Gulf with an inverted trough. Strong overrunning
Stratiform type event |
| Apr 8-9, 1998 | A cold front moved across state with squall line convective thunderstorms occurring ahead of the system |
| Aug 9, 1998 | There was moist air and a weak disturbance in the upper atmosphere causing thunderstorms. |
| Sept 3-4, 1998 | The remnants of Tropical Storm Earl produced heavy rains with embedded thunderstorms. |
.
Table 2.2 Number of Gauges Reporting During Each Precipitation
Event
| Rainfall Event | Manual Gauges | Tipping Gauges |
| Sept 24-28,1997 | 56 | 10 |
| Oct 22-26,1997 | 57 | 10 |
| Jan 22-23, 1998 | 58 | 10 |
| Feb 3-5, 1998 | 62 | 10 |
| Apr 8-9, 1998 | 58 | 10 |
| Aug 9, 1998 | 36 | 9 |
| Sept 3-4, 1998 | 48 | 8 |
Table 3.1 Interpolation Error Results for IDW and
Kriging
| Rainfall Events | Inverse Distance Weighting | Kriging | |
| Sept 24-28,1997 | Range:
Sum of Absolute Error: _______________________ ANOVA |
-1.96 to 2.7
5.22 inches _______________________ No Significant Difference |
-1.95 to 2.7
8.38 inches _______________________ No Significant Difference |
| Oct. 22-26,1997 | Range:
Sum of Absolute Error: _______________________ ANOVA |
-0.69 to 0.56
4.83 inches _______________________ No Significant Difference |
-0.69 to 0.51
5.18 inches _______________________ No Significant Difference |
| Jan. 22-23, 1998 | Range:
Sum of Absolute Error: _______________________ ANOVA |
-0.26 to 0.34
2.87 inches _______________________ No Significant Difference |
-0.26 to 0.28
2.29 inches _______________________ No Significant Difference |
| Feb. 3-5, 1998 | Range:
Sum of Absolute Error: _______________________ ANOVA |
-1.4 to 1.0
10.7 inches _______________________ No Significant Difference |
-1.3 to 1.1
10.29 inches _______________________ No Significant Difference |
| Apr. 8-9, 1998 | Range:
Sum of Absolute Error: _______________________ ANOVA |
-1.31 to 0.45
7.14 inches _______________________ No Significant Difference |
-1.06 to 0.40
6.81 inches _______________________ No Significant Difference |
| Aug. 9, 1998 | Range:
Sum of Absolute Error: _______________________ ANOVA |
-0.93 to 1.32
8.6 inches _______________________ No Significant Difference |
-0.82 to 1.46
7.92 inches _______________________ No Significant Difference |
| Sept. 3-4, 1998 | Range:
Sum of Absolute Error: _______________________ ANOVA |
-1.33 to 1.09
11.09 inches _______________________ No Significant Difference |
-1.39 to 0.98
10.35 inches _______________________ No Significant Difference |
*Note: Significance level = 0.05
Since the ANOVA proved no significant difference between interpolation
techniques the range and summed absolute error were used as criteria.
IDW used during Sep. 24-28, 1997, Oct. 22-26, 1997, Feb. 3-5, 1998
Kriging used during Jan. 22-23, 1998, Apr. 8-9, 1998, Aug. 9, 1998,
Sept. 3-4, 1998
Table 3.2 Rainfall Summary for Each Event
| Rainfall Event | Precipitation Range of All Gauges - inches | Radar Precipitation
Range of 157 NEXRAD Grids - inches |
| Sept. 24-28,1997 | 3.10 - 6.52 | 0 - 1.76 |
| Oct. 22-26,1997 | 0.87 - 3.02 | 0.09 - 0.79 |
| Jan. 22-23, 1998 | 0.98 - 2.22 | 0.06 - 0.66 |
| Feb. 3-5, 1998 | 2.93 - 4.23 | 0.23 - 1.31 |
| Apr. 8-9, 1998 | 0.88 - 2.64 | 0.30 - 2.67 |
| Aug. 9, 1998 | 0.25 - 2.13 | 0.04 - 1.96 |
| Sept. 3-4, 1998 | 4.94 - 7.35 | 1.67 - 4.94 |
Table 3.3 Root Mean Square Error For Each Event
|
|
|||
| Event |
|
||
| County | Outside 8 Miles of Radar | Inside 8 Miles of Radar | |
| Sept. 24-28, 1997 | 4.31 | 4.15 | 4.92 |
| Oct. 22-26, 1997 | 1.5 | 1.58 | 1.13 |
| Jan. 22-23, 1998 | 1.0 | 1.0 | 0.98 |
| Feb. 3-5, 1998 | 0.91 | 0.91 | 0.90 |
| Apr. 8-9, 1998 | 0.57 | .058 | 0.53 |
| Aug. 9, 1998 | 0.55 | 0.49 | 0.75 |
| Sep. 3-4, 1998 | 3.21 | 3.38 | 2.36 |
Table 3.4 Regression Model Output: R2 and F Statistic
|
|
||||||
| Event |
|
|
|
|||
| R2 | F Test | R2 | F Test | R2 | F Test | |
| Sep. 1997 | 0 | F=1.26
Pr>F 0.2625 |
0.10 | F=12.96
Pr>F 0.0005 |
0.02 | F=0.81
Pr>F 0.3753 |
| Oct. 1997 | 0.12 | F=20.37
Pr.F 0.0001 |
0.30 | F=51.38
Pr>F 0.0001 |
0.02 | F=0.58
Pr>F 0.45 |
| Jan. 1998 | 0.52 | F=169.60
PR>F 0.0001 |
0.57 | F=159.89
Pr>F 0.0001 |
0.66 | F=68.78
Pr>F 0.0001 |
| Feb. 1998 | 0.11 | F=18.85
Pr>F 0.0001 |
0.27 | F=43.32
Pr>F 0.0001 |
0 | N/A |
| Apr. 1998 | 0 | N/A | 0.01 | F=0.69
Pr>F 0.4070 |
0.12 | F=4.99
Pr>F 0.0321 |
| Aug. 1998 | 0 | F=3.36
Pr>F 0.0689 |
0 | N/A | 0 | N/A |
| Sep. 1998 | 0.02 | F=2.87
Pr>F 0.0922 |
0.03 | F=4.01
Pr>F 0.0477 |
0.03 | F=1.125
Pr>F 0.2964 |
Table 3.5 RMSE and Regression Output for Twelve Mile Creek
and Fourteen Mile Creek Basin
|
|
|||
| Event | Root Mean Square Error (inches) | R2 | F Test |
| Sept. 24-28, 1997 | 4.90 | 0.27 | F=7.551
Pr>F 0.0124 |
| Oct. 22-26, 1997 | 1.29 | .048 | F=18.591
Pr>F 0.0003 |
| Jan. 22-23, 1998 | 0.78 | 0.15 | F=3.496
PR>F 0.0762 |
| Feb. 3-5, 1998 | 2.81 | 0.12 | F=2.737
Pr>F 0.1136 |
| Apr. 8-9, 1998 | 0.87 | 0.22 | F=5.481
Pr>F 0.0297 |
| Aug. 9, 1998 | 0.50 | 0.03 | F=0.593
PR>F 0.4502 |
| Sep. 3-4, 1998 | 3.36 | 0.87 | F=132.409
Pr>F 0.0001 |
Figure 1.1 Radar Scan Angles (degrees) and Volume Scanning Technique
(WSR-88D Operations Training Student Guide, 1993)

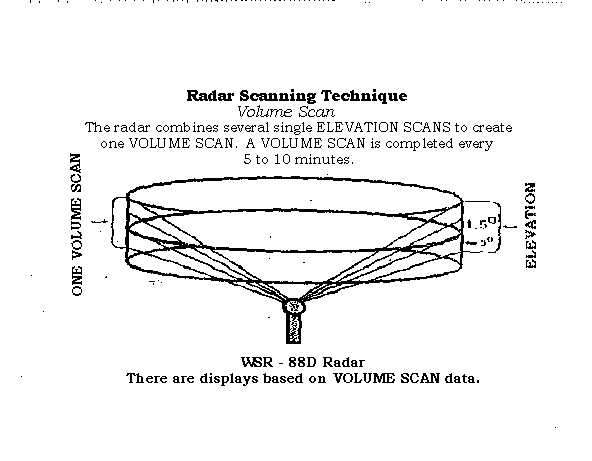
Figure 1.2 Example of Radar Bin and Reflectivity Correction
Techniques
(WSR-88D Operations Training Student Guide, 1993)
Removes reflectivity outliers that can cause precipitation overestimation.
A range bin is flagged as an outlier if its reflectivity value exceeds
the current outlier threshold (MXRFL, 65 dBZ).
If all eight neighboring range bins have values below MXRFL,
the outlier is replaced by the average of the eight neighbors.
Figure 2.1 Description of Tipping Gauge Calibration and Recording Techniques
(UNIDATA Equipment Manual, 1996)
Model: UNIDATA 6506B Rain Gauge

Calibrated to 0.01 inches
Sensor consists of a gold anodized aluminum collector funnel with a
knife edge that diverts water to a tipping bucket mechanism. The
mechanism is designed so that one alternate tip of the bucket occurs for
each 0.01 inch of rainfall. A magnet is attached to the tipping bucket
which, as the bucket tips, actuates a magnetic switch. A momentary
switch closure takes place with each tip of the bucket. The sensor
is connected to an event counter on an electronic datalogger which records
the accumulated rainfall. The spent water then drains out of the
bottom of the housing unit.
/* This program is intended to decode the hdp array as it comes from
/* NWI, according to the document CDRL 221, Communications Interface Users
/* Guide.
/*
/* This program reads in the HDP array and writes a comma delimited
/* text file to standard output to go along with the fishnetutm coverage.
/* The dba values from the HDP (hourly digital precpitation) have to be
/* converted to inches of precip. The program dechdp.c is Chuck Little's
/* adaptation of a program written by Robert Shedd. That program contains
/* an algorithm for converting from dba to inches, which is used here.
/*
/* Michael Braun
/* July 22, 1997
*/
#include "stdio.h"
#include "string.h"
#include "math.h"
#include "stdlib.h"
void main (int argc, char *argv[])
{
FILE *Infile;
int I, J, LastJ, Fishnet_ID, Output, Lastoutput, date, year, month, day, hour;
signed short int Pcode, X, X2,
Packcode, Numbytes, Bytes, Numrows, Numcolumns, Dba[132][132],
Runlength, Level, IMax_dba, Omode;
signed short int IMin_dba, IDba_inc, Dba_levels;
unsigned char Runlengthc, Levelc;
float Max_dba, Min_dba, Dba_inc, Dbaf[132][132], Inches[132][132];
if (argc!=2) {
printf("Wrong number of parameters.\n");
printf("command: rdhdp \n");
exit(0);
}
if ((Infile=fopen(argv[1],"r"))==NULL) {
printf("Cannot open %s\n",argv[1]);
exit(0);
}
/* get time from file name */
date=atoi(argv[1]);
hour=date%100;
date=date/100;
day=date%100;
date=date/100;
month=date%100;
date=date/100;
year=date;
Appendix 2.1 C program to decode binary WSR-88D data (continued)
/* Read product description block */
fread(&Pcode,2,1,Infile);
if (Pcode!=81) {
printf("Pcode = %i\n",Pcode);
printf("%s is not an hourly digital precipitation file.\n",argv[1]);
exit(0);
}
for (I=1;I<=15;I++) fread(&X,2,1,Infile);/* skip ahead 2*15 bytes */
fread(&Omode,2,1,Infile);
if (Omode!=2) {
printf("Omode = %i\n",Omode);
printf("%s is not in precipitation mode.\n",argv[1]);
exit(0);
}
for (I=1;I<=13;I++) fread(&X,2,1,Infile);/* skip ahead 2*13 bytes */
fread(&IMin_dba,2,1,Infile);
Min_dba=IMin_dba/10.0;
fread(&IDba_inc,2,1,Infile);
Dba_inc=IDba_inc/1000.0;
fread(&Dba_levels,2,1,Infile);
/* printf("Mindba=%f dbainc=%f dbalevels=%i\n",Min_dba,Dba_inc,Dba_levels);
*/
/* Read max dba */
for (I=1;I<=13;I++) fread(&X,2,1,Infile);/* skip ahead 2*14 bytes */
fread (&IMax_dba,2,1,Infile);
Max_dba=IMax_dba*0.1;
/* printf("Max dba= %f\n",Max_dba);
*/
/* Skip to symbology block. */
while (X!=1&&X2!=-1) {
X2=X;
fread(&X,2,1,Infile);
}
while (X!=-1) fread(&X,2,1,Infile);
fread(&X,2,1,Infile);
fread(&X,2,1,Infile);
fread(&Packcode,2,1,Infile);
if (Packcode!=17) {
printf("Packet Code for symbology data is not 17.\n");
exit(0);
}
fread(&X,2,1,Infile);
fread(&X,2,1,Infile);
fread(&Numcolumns,2,1,Infile);
fread(&Numrows,2,1,Infile);
if (Numcolumns!=131||Numrows!=131) {
printf("Wrong number of columns or rows in grid.\n");
exit(0);
}
/* Read in dba data */
for (I=Numrows;I>=1;I--) {
fread(&Numbytes,2,1,Infile);
LastJ=1;
Appendix 2.1 C program to decode binary WSR-88D data (continued)
Bytes=2;
while (Bytes<=Numbytes) {
fread(&Runlengthc,1,1,Infile);
Runlength=Runlengthc;
fread(&Levelc,1,1,Infile);
Level=Levelc;
for (J=LastJ;J<=(LastJ+Runlength-1);J++) {
Dba[I][J]=Level;
}
LastJ=LastJ+Runlength;
Bytes=Bytes+2;
}
}
/* Convert to inches and output. */
printf("Fishnet-ID,Inches\n");
for (I=1;I<=131;I++) {
for (J=1;J<=131;J++) {
if (Dba[I][J]==0) { /* no accumulation */
Dbaf[I][J]=0;
Inches[I][J]=0;
}
else if (Dba[I][J]==255) { /* outside range */
Dbaf[I][J]=-9999;
Inches[I][J]=-9999.99;
}
else {
Dbaf[I][J]=Min_dba+(Dba[I][J]*Dba_inc);
/* printf("Dba: %f :level=%i\n",Dbaf[I][J],Dba[I][J]);
*/
/* if (Dbaf[I][J]<=0.0) Inches[I][J]=0;
else
*/ Inches[I][J]=(pow(10.0,(Dbaf[I][J]/10.0))/25.4);
}
Fishnet_ID=131*(I-1)+J;
Output=(I<=78)&&(I>=54)&&(J<=81)&&(J>=57);
Lastoutput=(Fishnet_ID==10299);
if (Output) {
printf("%5i,",Fishnet_ID);
printf("%7.2f\n",Inches[I][J]);
}
}
}
fclose(Infile);
}
Appendix 2.2 Avenue Script for Universal Kriging Interpolation Technique
' 1. Interpolate Grid using Universal Kriging
' by: Hope Mizzell'
' 2-16-99
'--Get the active view document---
theView = av.GetActiveDoc
'--Make a list of the themes in Active view -----
themeList = List.Make
for each t in theView.GetThemes
theme.List.Add(t)
end
'--Pop up a message box to select gauge coverage ----
theTheme = MsgBoxx.LIST(themeList, "Pick Gauge Grid:", "Gauges")
themeList.RemoveObj(theTheme)
'-Set up grid analysis environment, extent, and cell size ----
themeExtent = theTheme.ReturnExtent
Grid.SetAnalysisExtent(#GRID_ENVTYPE_VALUE, themeExtent)
Grid.SetAnalysisCellSize(#GRID_ENVTYPE_VALUE, 100)
'--Prepare Parameters for Kriging Interpolation----
StationFTab = theTheme.GetFTab
StationPrj = Prj.MakeNull
KrigInterp = Interp.MakeKriging(#KRIGING_UNIVERSAL1, 3, Nil, kriggrd)
'--construct an appropriate field name---
Field = StationFTab.FindField(Sep 24-28'97)
'--Do Kriging Interpolation---
PrecipGrid=Grid.MakeByInterpolation(StationFTab,StationPrj,Field,KrigInterp,NIL)
'--Add Precipitation Theme to the View---
PrecipTheme=GThem.Make(PrecipGrid)
PrecipTheme.SetName("Kriging Surface")
theView.AddTheme(PrecipTheme)
Appendix 2.3 SAS ANOVA for Testing Significance of
Interpolation Technique Errors
Data IDWKrig;
Title1 'ANOVA to Test Interpolation Techniques Errors - IDW & Kriging';
Input error int $;
Cards;
-0.36 i
-0.39 i
0.14 i
0.26 i
0.14 i
-1.31 i
-0.1 i
0.02 i
0.1 i
0.05 i
-0.62 i
0.31 i
-0.34 i
(Numbers Omitted to Conserve Space)
-0.12 k
-0.05 k
0.3 k
0.2 k
;
Proc ANOVA;
Class int;
Model error=int;
Means int /SNK;
Run;
Appendix 2.4 Avenue Script for Computing Root Mean Square Error
' ---- THIS IS A SCRIPT FOR Computing RMSE for County --
' Name: rmsecnty.ave
' Author: Hope Mizzell'----------------------------------------
'--- GET THE ACTIVE VIEW DOCUMENT ----
theView = av.GetActiveDoc
'--- MAKE A LIST OF THE THEMES IN ACTIVE VIEW---
themeList = List.Make
for each t in theView.GetThemes
themeList.Add(t)
end
' --- Retrieve the Active Theme
xtheme = MsgBox.List(ThemeList, "Pick x Grid:", "X Grid")
if (xtheme = NIL) then return NIL end
xgrid = xtheme.getgrid
'--------- Remove Grid x THEME and Pick y GRID -----
ThemeList.RemoveObj(xtheme)
ytheme = MsgBox.List(ThemeList, "Pick y Grid:", "Y Grid")
if (ytheme = NIL) then return NIL end
ygrid = ytheme.getgrid
'--------- Remove Grid y THEME and Pick Zone GRID -----
ThemeList.RemoveObj(ytheme)
zonetheme = MsgBox.List(ThemeList, "Pick zone Grid:", "Zone Grid")
if (zonetheme = NIL) then return NIL end
zone = zonetheme.getgrid
zoneVTab = zone.GetVTab
'get zone Field from zoneObj
zoneField = zoneVTab.FindField("Value")
diffgrid = ygrid - xgrid
difftheme = GTheme.Make(diffgrid)
difftheme.SetName("Nex-Int")
theView.AddTheme(difftheme)
Appendix 2.4 Avenue Script for Computing Root Mean Square Error (continued)
diffsqrgrid = diffgrid.sqr
diffsqrtheme = Gtheme.Make(diffsqrgrid)
Appendix 2.4 Avenue Script for Computing Root Mean Square Error (cont.)
diffsqrtheme.SetName("Nex-Int Squared")
theView.AddTheme(diffsqrtheme)
Sum = diffsqrgrid.ZonalStats(#GRID_STATYPE_SUM, zone, Prj.MakeNull, zonefield, False)
Sumtheme = GTheme.Make(Sum)
Sumtheme.SetName("Sum of Diff Squared")
theView.AddTheme(Sumtheme)
'return 0
MSE = Sum/195946
MSEtheme = GTheme.Make(MSE)
MSEtheme.SetName("MSE")
theView.AddTheme(MSEtheme)
RMSE = MSE.sqrt
'Add RMSE to View'
RMSEtheme = GTheme.Make(RMSE)
RMSEtheme.SetName("RMSE")
theView.AddTheme(RMSEtheme)
exit
Appendix 2.5 Avenue Script for Summarizing by Zone
' ---- THIS IS A SCRIPT FOR Summarizing by Zone --
' Name: sumintzon.ave
' Author: Hope Mizzell'----------------------------------------
'--- GET THE ACTIVE VIEW DOCUMENT ----
theView = av.GetActiveDoc
'--- MAKE A LIST OF THE THEMES IN ACTIVE VIEW---
themeList = List.Make
for each t in theView.GetThemes
themeList.Add(t)
end
' --- Retrieve the Active Theme
xtheme = MsgBox.List(ThemeList, "Pick x Grid:", "X Grid")
if (xtheme = NIL) then return NIL end
xgrid = xtheme.getgrid
'--------- Remove Grid x THEME and Pick Zone GRID -----
ThemeList.RemoveObj(xtheme)
zonetheme = MsgBox.List(ThemeList, "Pick zone Grid:", "Zone Grid")
if (zonetheme = NIL) then return NIL end
zone = zonetheme.getgrid
zoneVTab = zone.GetVTab
'get zone Field from zoneObj
zoneField = zoneVTab.FindField("Value")
intmean = xgrid.ZonalStats(#GRID_STATYPE_MEAN, zone, Prj.MakeNull, zonefield, False)
intmeantheme = GTheme.Make(intmean)
intmeantheme.SetName("Int Mean")
theView.AddTheme(intmeantheme)
exit
Appendix 2.6 SAS Regression Model
Title1 'Regression Model';
Title2 'NEXRAD Estimated Precipitation and Gauge Interpolations Averaged By NEXRAD Grid';
Data PRECIP;
Input GRIDID NEXRAD GAUGE;
LNEXRAD=LOG(NEXRAD);
LGAUGE=LOG(GAUGE);
Cards;
7137 0.2000 0.9786
7138 0.4000 0.9654
7142 0.8500 0.7778
7143 0.8302 0.7153
7265 0.4800 0.9568
7266 0.5500 0.8432
7267 0.1400 0.9269
7268 0.2000 0.9417
7269 0.5282 0.8982
7272 0.5101 1.0480
(Numbers Omitted to Conserve Space)
8706 0.4544 0.3080
8707 0.6343 0.2955
8710 1.0420 0.5716
8711 1.0880 0.6668
8837 0.4215 0.3016
8838 0.4562 0.3006
;
Proc CORR;
Var LNEXRAD LGAUGE;
Run;
/*Regression With GAUGE and NEXRAD*/
Proc Reg Data=PRECIP;
/*Model dependent = regressor variable*/
Model LNEXRAD=LGAUGE / R RMSE Selection=Forward CORRB STB TOL;
ID GRIDID;
Run;
Appendix 2.7 SAS ANOVA for Testing Significance of Radar-Gauge Differences for All Events
Data Diff;
Title1 'ANOVA to Test Percent Difference NEXRAD and Gauge for All Events';
Input percent month $;
Lpercent=LOG(percent);
Cards;
12.15883 sep
15.5814 sep
21.34496 sep
27.75229 sep
18.73431 sep
14.10093 sep
15.43967 sep
15.29106 sep
15.29242 sep
12.77415 sep
16.2793 sep
(Numbers Omitted to Conserve Space)
74.72341 earl
32.95319 earl
35.12078 earl
39.05834 earl
63.01005 earl
75.67939 earl
36.95277 earl
35.3015 earl
50.43229 earl
;
Proc ANOVA;
Class month;
Model Lpercent=month;
Means month /SNK;
Run;